|
|
|
Charles Dougherty Dougherty 1
Mrs. Sheppard
AP Calculus BC
June 2007
Quartic functions, polynomials with a degree of four, come in many different varieties one of which is the “W” shaped function.. When the “W” shaped function is assigned two points of inflection, Q and R and a line is drawn through those points to meet the quartic function at points P and S a common ratio can be found between PQ:QR:RS. To support this idea of a common ratio lets first look at the function:
![]()
Our first order of business will be to identify points Q and R.
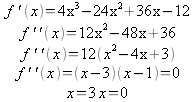

![]()
Looking at the results there are inflection points at x=3 and x=0 where the function goes from concave up to concave down and back to concave up.
![]()
![]()
Now that the coordinates of the inflection points Q and R have been found they can be used to find the equation of the line that intersects the graph.
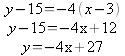
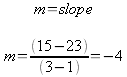
By setting the two equations equal to each other and/or making use of the intersect function on the TI-83 the points of intersection can be found which tells what points P and S are.
![]()
By using the points P,Q, R, and S a relationship can be found using the horizontal (x) distance between each of the points.

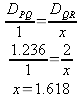 Based
off of these numbers PQ:QR:RS is equal to 1.236:2:1.236 with PQ = QR.
By assigning PQ a value of 1 a new ratio can be formed.
Based
off of these numbers PQ:QR:RS is equal to 1.236:2:1.236 with PQ = QR.
By assigning PQ a value of 1 a new ratio can be formed.
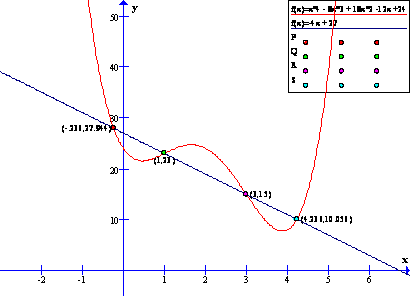
The new ratio of PQ:QR:RS is 1:1.618:1. Based off of these findings it can be inferred that perhaps the distance from PQ and RS is always equal in “W” shaped functions. The best way to find out is to check the ratio on another function.
Without a specified function a new one must be created. Stating with the inflection points x = 2 and x = 4 a second derivative function can be created and then integrated to find a new “W” shaped function.
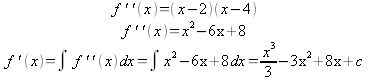
Because integrating indefinite integrals yields an integration constant the problem of how to deal with said constant arises. The best way to handle this is to consider what is already know; it is known that it is a “W” shaped, it is also known that because of this the derivative has to change three times from negative to positive to negative to positive in order based off of this it can assume that there are three points in which the derivative of f is equal to zero. Finally it is also known that because of how “W” shaped quartic functions appear the slope changes just before and just after the inflection points. By combining these facts it can be surmised that there is a point before the inflection point at x =2 in which the derivative of f is equal to zero, there is also a point between the inflection points at x =2 and x =4 in which the derivative of f is equal to zero, finally just after the inflection point at x =4 there is a point in which the derivative of f is equal to zero. With this information an arbitrary number, in this case x = 3 can be chosen and made to fit into those conditions so that C can be solved for.
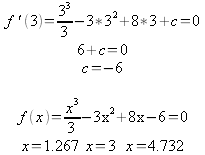
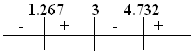
![]()
After inspecting the extrema the aforementioned conditions held true and the function is ready for integration..
![]()
Once again a constant of integration appears in the results, however since it is in the final function and the “+d” simply shifts the function upwards it can be dropped from the equation since the investigation is inspecting the horizontal distance which is independent of any vertical shifts the function may make.
![]()
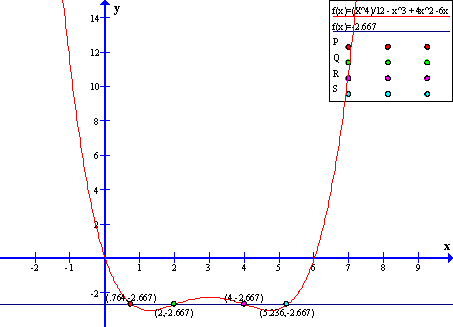
That being done Q and R can now be found, followed by the equation of the line that intersects the function.
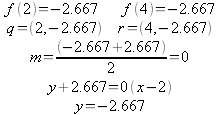
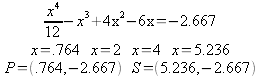 Setting
the equations equal to each other and making use of a graphing
utility the points of intersection are once again found, P and S
along with them.
Setting
the equations equal to each other and making use of a graphing
utility the points of intersection are once again found, P and S
along with them.
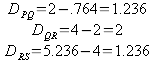
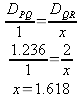
The results above maintain the same ratio that was yielded when working with the previous quartic function. The similar results support the hypothesis that the horizontal distance from P to Q and R to S will always be equal. Since the ratios are the exact same a the hypothesis can be appended to say that not only will the distance from P to Q and R to S will always be equal, but also that the the distances P to Q, Q to R, and R to S will maintain a ratio of 1:1.618:1.
The hypothesis can be supported by working with a quartic function in the general form. To begin point P will be set to the origin (0,0) and the second inflection point will be at “a”. From here the second derivative can be found and integrated.
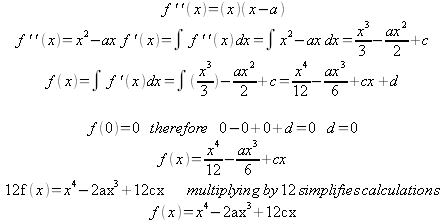
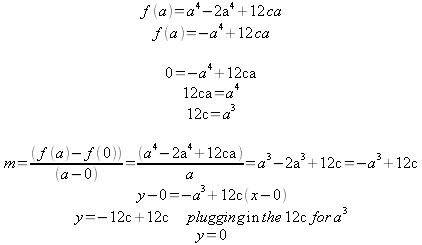 With
f(x) point f(a) can be found and the equation of the intersecting
line.
With
f(x) point f(a) can be found and the equation of the intersecting
line.
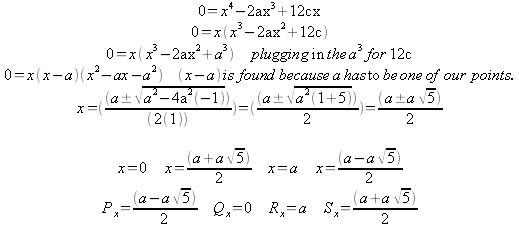 The
intersecting points are once again found by setting the two equations
equal to each other.
The
intersecting points are once again found by setting the two equations
equal to each other.
With the X values of P, Q, R and S found the horizontal distance can be found and then the ratios checked.
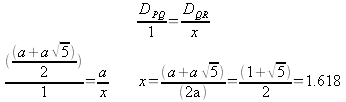
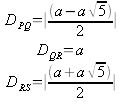
Looking at the results it is once again obvious that the ratio holds true and therefore it can be concluded that for “W” shaped quartic functions there is a common ratio of 1:1.618:1 for PQ:QR:RS when Q and R are assigned to the inflection points of the function and a line is drawn through Q and R to meet the function once again at points P and S. This investigation can be further extended to functions which are not strictly “W” shaped. One of the most obvious places to look is at an “M” shaped function which is merely the inverse of a “W” shaped quartic function.
Looking quickly at the general form of the following function it is once again obvious that the distances between QR and RS are once again equivalent and further the entire ratio is sustained.
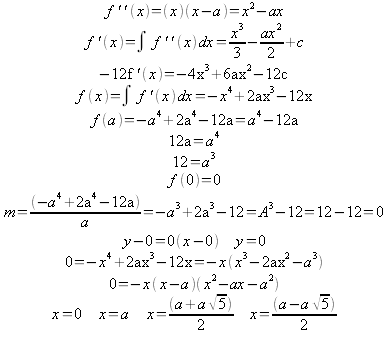
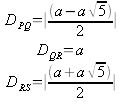
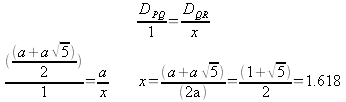
Without Introducing another function to manipulate the quartic function (ex: f(x)=g(x)4) the only other shapes that can be produced by a quartic function are the “U” shape and the “n” shape, both of which lack inflection points which would be necessary to apply the investigation to them.
Based off of the results of the investigation it can be concluded that quartic functions with two inflection points will have a PQ:QR:RS ratio of 1:1.618:1. It is somewhat significant to point out that the number 1.618 is a good approximation of the mathematical number phi(φ) which is renowned for popping up in obscure places.